Blogpost vom 23. Mai 2019
Quantencomputer und IT-Sicherheit
Um mehr Leistung in Computer packen zu können, müssen dessen Teile immer kleiner werden. In naher Zukunft erreichen wir Maßstäbe, die sich unter der Größe von Atomen befinden – und wo ganz andere Regeln gelten: Dort verlassen wir nämlich das Reich der klassischen Physik und betreten die Sphäre der Quantenphysik.
Computer, die in diesem Maßstab gebaut werden, unterscheiden sich fundamental. Sie basieren nicht mehr auf festen Ergebnissen, die entweder klar 0 oder klar 1 sind, sondern auf Wahrscheinlichkeiten.
Wo ein klassischer Computer auf Bits setzt, die entweder 0 oder 1 sind, basiert ein Quantencomputer auf Quanten-Bits, kurz Qubits genannt. Diese unterscheiden sich dadurch, dass sie sowohl einen Wert 0 oder 1 einnehmen können als auch einen Wert dazwischen – mehr dazu später. Qubits sind jedenfalls die Eingaben für die Schaltungen der Quantencomputer, auf ihnen rechnet das System. Die Schaltungen selbst werden Quantengatter genannt.
Technologietrend Quantencomputer
In den letzten Jahren hat sich einiges getan auf dem Gebiet. Die Hauptakteure 2019 sind die USA und China, wobei die EU nachzieht. Präsident Trump unterzeichnete im Dezember 2018 den National Quantum Initiative Act, dessen Plan es ist, die Technologie in den nächsten 10 Jahren in den USA maßgeblich voranzutreiben. Google veröffentlichte 2018 einen 72-QuBit-Rechner namens Bristlecone, und IBM bietet über “Q Experience” nunmehr direkten Zugriff auf Quantencomputer via Cloud für jedermann. Der zuletzt herausgebrachte „IBM Q System One“ ist erstmals ein Quantencomputer, der speziell für den wirtschaftlichen Einsatz gedacht ist. Die EU stellte 2018 ihrerseits 9,1 Millionen Euro für die Forschung zum Thema bereit. Gartner, ein Anbieter für Marktforschung, listet Quantum Computing als eines der Top 10 strategischen Technologietrends für 2019.
Was bedeuten Quantencomputer für die IT-Sicherheit?
Mit Quantencomputern könnten bestimmte IT-Probleme künftig wesentlich effizienter gelöst werden als mit klassischen Rechnern. Das betrifft große Simulationen, Optimierungs- und Klassifizierungsprobleme ebenso wie Algorithmen für große Datenmengen sowie insbesondere Kryptographie und Kryptoanalyse.
Kryptographie hat die Aufgabe, Informationen verschlüsselt zu übertragen und nach Empfang wieder zu entschlüsseln. Die Kryptoanalyse ist gegenteilig ausgelegt: Ihr geht es um das Brechen von Verschlüsselungen, ohne das dies von Sender und Empfänger gewollt bzw. bemerkt wird.
Derzeit basiert die Kryptographie im Wesentlichen auf der Grundlage, dass gewisse mathematische Probleme nicht leicht zu lösen sind – und sich Angriffe schon wegen des hohen Rechenaufwands nicht lohnen.
Mit Quantencomputern hingegen können viele mathematische Probleme in so kurzer Zeit gelöst werden, dass die zeitgenössische Kryptographie allein nicht mehr ausreicht.
Der Quantencomputer als Rechengenie
Wo ein herkömmlicher Rechner entweder Nullen oder Einsen zur Verfügung hat, um Dinge zu berechnen, hat ein Quantencomputer die 0 und die 1 gleichzeitig zur Verfügung. Das heißt, er kann parallel auf beiden Zuständen rechnen. Oder anders ausgedrückt: Ein Algorithmus rechnet sowohl das Ergebnis für 0 als auch das Ergebnis für 1 in einem Schritt aus.
- Bei 2 Bits sind das vier Zustände, auf denen parallel gerechnet wird: 00,01,10 und 11.
- Bei 3 Bits sind es dann schon 8 Zustände: 000,001,010,011,100,101,110 und 111.
Insgesamt ergibt sich so ein exponentielles Wachstum des Berechnungsraums von 2x, mit x der Anzahl der Qubits.
Beispiel RSA
Um das Problem besser zu verstehen, schauen wir uns an, wie eines der großen Kryptographieverfahren im Kern funktioniert: RSA. Dieses findet man heutzutage in vielen Anwendungsbereichen, etwa bei der Verschlüsselung des Internets, von Telefonen, E-Mails oder im Electronic Banking.
RSA basiert auf der Schwierigkeit, eine Zahl, die aus einer Multiplikation entstanden ist wieder in die ursprünglichen 2 Zahlen zu zerlegen. Diese ursprünglichen 2 Zahlen sind speziell: Man kann sie nur durch sich selbst oder 1 teilen. Beispiele sind 2,3,5 oder 7.
Der naheliegende Weg, a und b zu finden, ist alle Multiplikationen durchprobieren, bis wir am Ende c finden – was mit steigender Größe der Zahlen immer komplizierter wird, denn die Komplexität wächst dabei aufgrund der Menge möglicher Primzahlen besonders schnell.
Selbst die schnellsten bekannten Algorithmen für klassische Computer können das Problem angesichts des Wachstums ab einer bestimmten Zahlengröße nicht mehr lösen.
Der Shor-Algorithmus
Anders Quantencomputer. Für diese gibt es einen Algorithmus, der die Lösung in wesentlich kürzerer Zeit liefern kann: der Shor-Algorithmus. Dieser wurde 2001 erstmals experimentell für die Zahl 15 durchgeführt, die damit erfolgreich in die Zahlen 3*5 zerlegt wurde.
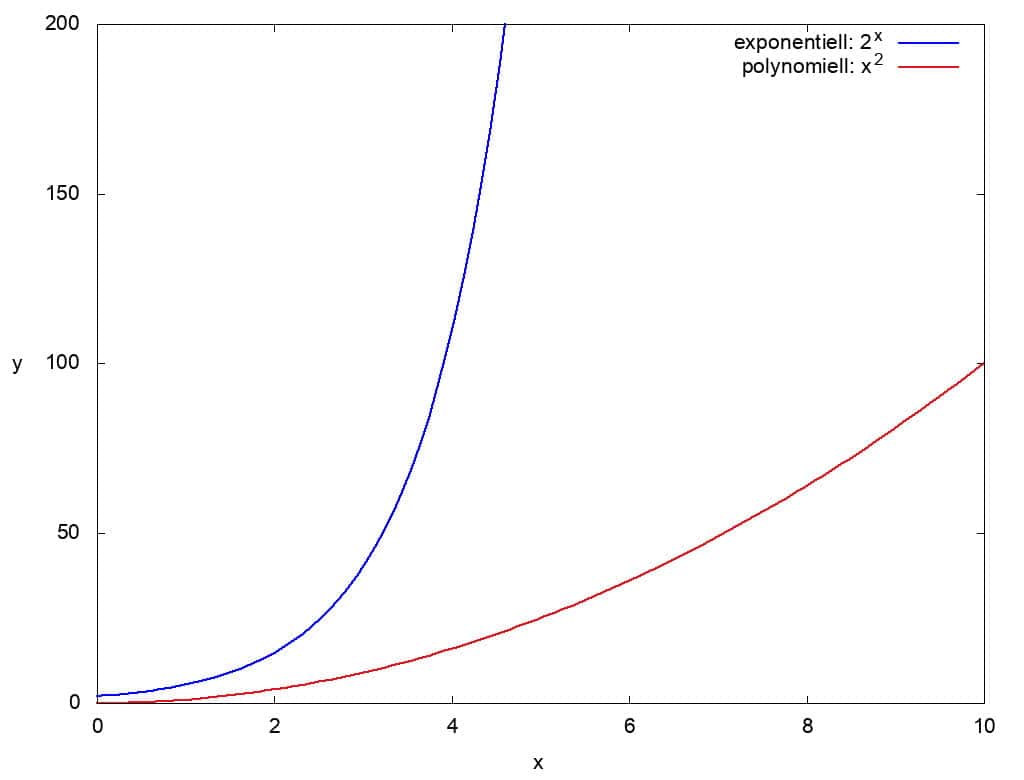
Das nachfolgende Bild zeigt grob skizziert, wie man sich den Unterschied zwischen klassischem und Quantencomputer vorstellen kann. Dabei unterscheidet man den exponentiellen Aufwand vom polynomiellen. Klassische Computer benötigen exponentiell viel Aufwand für die Primfaktorzerlegung, Quantencomputer polynomiell viel. In der Darstellung werden 2 Funktionen aus diesen beiden Klassen gezeigt: 2x und x². In der Realität sind die Funktionen für den Aufwand in beiden Algorithmen komplexer aufgebaut. Die hier gewählten einfacheren Funktionen sollen zur Veranschaulichung des Unterschieds dienen.
Der Shor-Algorithmus kann aber noch mehr. Er bricht neben RSA auch andere gängige Kryptographieverfahren: Elliptische Kurven und diskrete Logarithmen.
Für RSA benötigt er eine Mindestanzahl von Qubits: 2n+3, wobei n die Anzahl der Bits derjenigen Zahl ist, die zu faktorisieren ist. Das heißt: Wurde RSA mit einer Zahl versehen, die mit 1024 Bits dargestellt werden kann, so benötigt der Shor-Algorithmus mindestens 2*1024+3 = 2050 Qubits, um diese Zahl effizient zu zerlegen.
Auch die Kryptographie entwickelt sich weiter
Zum Glück hat sich auch die Kryptographie weiterentwickelt, weil das Problem frühzeitig erkannt und beforscht wurde. Aus dieser Forschung sind kryptographische Methoden hervorgegangen, die auch Quantencomputern standhalten können. Diese Form der Kryptographie wird Post-Quantum-Kryptographie genannt. Zum Teil sind ihre Methoden schon heute in gängigen Kommunikationstools wie SSH vorgesehen.
Experimente mit Quantencomputern
Wer Lust hat, mal ein bisschen mit Quantencomputern herumzuspielen, kann sich einen Account bei IBM anlegen und direkt auf einem Quantencomputer Schaltungen erzeugen, die dann über die Cloud auf IBM Q Experience gesendet werden können.
Zudem gibt es eine Menge aufkommender Programmiersprachen, die Quantencomputer simulieren können und mittelfristig für dessen Programmierung gedacht sind. Beispiele hierfür sind Microsoft Azure Q#, Project Q und Qiskit für Python oder Cirq.
Hier ein paar Ideen zum Einsteigen:
Man könnte zum Beispiel mit einem leeren System anfangen, das komplett mit Nullen initialisiert ist und einfach gemessen wird:
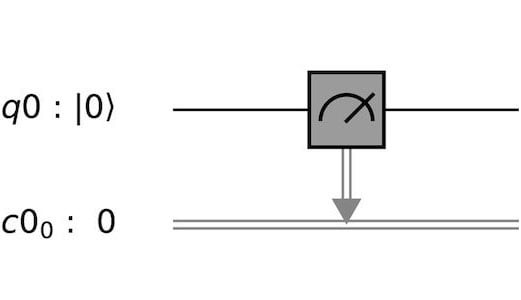
Messung eines Qubits (q0) und Übertragung des Ergebnisses auf ein klassisches Bit (c0)
… Oder einfach mal ein Qubit negieren:
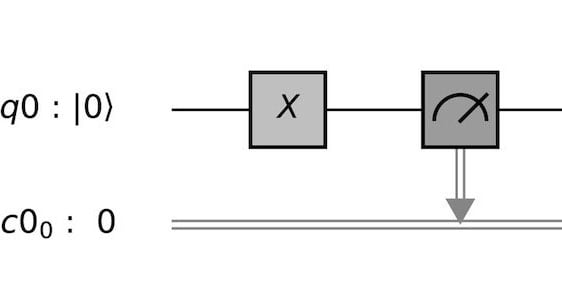
Qubits werden mittels eines Pauli-X-Gatters negiert
Der wichtigste, aber auch schwierigste Schritt ist, zu verstehen, wie man das System in den Modus versetzt, dass auf allen Qubits gleichzeitig gearbeitet wird. Hierfür ist das Hadamard-Gatter der erste Anlaufpunkt:
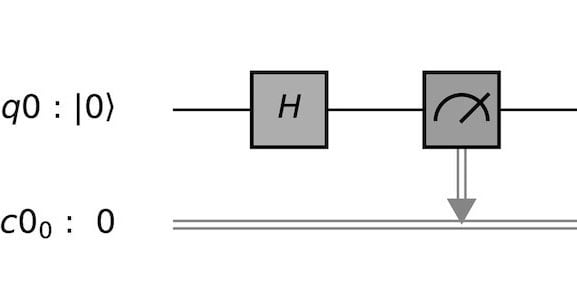
Hadamard-Gatter, um auf Qubits gleichzeitig 0 und 1 zu rechnen
Fazit
Grundsätzlich müssen wir Softwareentwickler uns darauf einstellen, dass die Dinge hier ein wenig anders laufen, als wir es gewohnt sind. Wichtig ist, dass wir uns davon nicht abschrecken und der Sache offen gegenüberstehen. Einen übersichtlichen, praktischen Einstieg mit Links bietet zum Beispiel diese Awesome List auf Github.
Insgesamt bleibt die Entwicklung von Quantencomputern ein Thema, das derzeit in Forschung und Wirtschaft stark bearbeitet wird. Wir werden sehen, was die Zukunft bringt. Es dürfte spannend bleiben.





