Blogpost vom 11. April 2024
Das Perceptron: Urgestein der modernen KI
In dem hochdynamischen Feld der modernen KI sind künstliche Neuronen einer der wichtigsten Grundbausteine. Jedes neuronale Netz besteht aus verschiedenen Schichten dieser Neuronen, welche grob gesagt miteinander interagieren, um beliebige Funktionen zu lernen. Die älteste Art dieser Neuronen ist das Perceptron. Um die grundsätzliche Funktionsweise und die Entstehung des Preceptrons zu verstehen, müssen wir zunächst eine kurzen Ausflug in die 1940er und 1950er machen.
Von einer Idee hin zur ersten Implementierung
Warren S. McCulloch und Walter Pitts veröffentlichen 1943 das Werk „A logical calculus of the ideas immanent in nervous activity“1, in dem sie ein logisches Element vorstellen, welches mehrere Eingangs- und genau ein Ausgangssignal hatte. Die Berechnung des Ausgangssignals war dabei relativ einfach: Falls die Summe der Eingabesignale einen vorgegebenen Schwellwert überschreitet, wird 1 ausgegeben, andernfalls 0.
Ein weiterer wichtiger Grundbaustein ist die Hebbsche Lernregel2, welche 1949 von Donald Olding Hebb veröffentlicht wurde. Sie beschreibt die Veränderungen der Verbindung zwischen Neuronen beim Lernen. Vereinfacht gesagt wird die Verbindung zwischen zwei Neuronen verstärkt, wenn sie häufiger gleichzeitig aktiv sind. Je stärker diese Verbindung ist, desto stärker reagieren die Neuronen aufeinander.
Der nächste große Schritt erfolgte durch Frank Rosenblatt durch die Veröffentlichung des Perceptron Modells, welches die Ergebnisse von McCulloch & Pitts mit den Ergebnissen von Hebb vereinigt und somit die Grundlage der meisten modernen Neuronalen Netzwerken geschaffen hat. Grundlegend werden dabei Eingabesignale mit Gewichten multipliziert. Falls deren Summen einen definierten Schwellwert überschreiten, wird eine logische 1, andernfalls eine logische 0 ausgegeben.
Die erste Implementierung des Modells erfolgte 1958 zunächst als Software, aber auch als eigenständige Maschine, dem „Mark 1 Perceptron“. Das Mark 1 Perceptron bestand aus 400 Fotozellen, welche als Eingabesignale dienten, Potentiometern, die die Gewichte simulierten und elektrische Motoren, die das Anpassen der Gewichte ermöglichten. Somit können einfache geometrische Formen wie Kreise, Dreiecke, Rechtecke oder Buchstaben erkannt werden.
Wie funktioniert ein Perceptron?
Eingabesignale
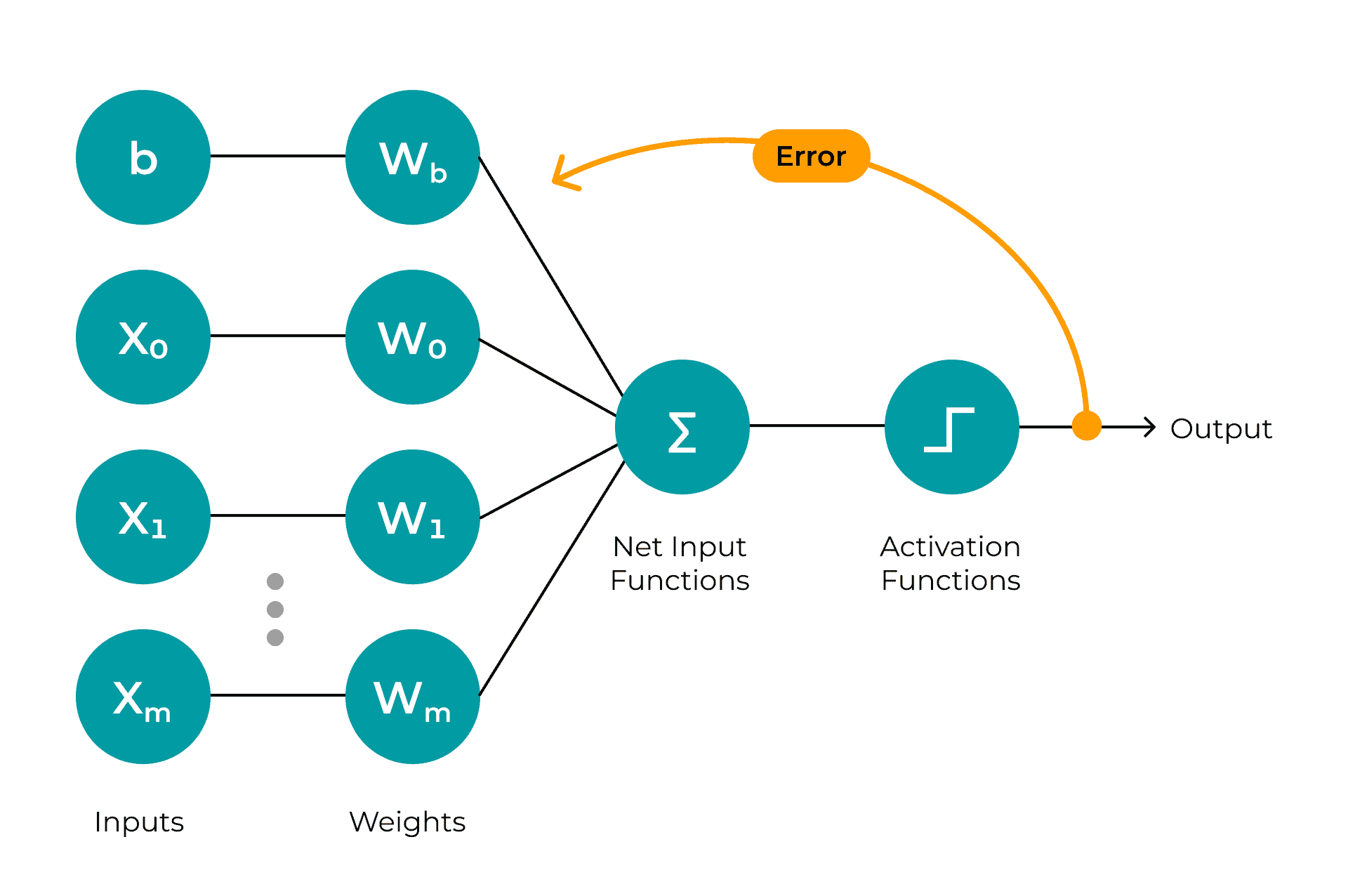
Die Eingabesignale bilden die erste Schicht des Perceptrons. Typischerweise handelt es sich hier um numerische Werte, da sie die nachfolgenden Berechnungen vereinfachen. Kategorische Werte müssen vorher also in numerische Werte überführt werden. Für jedes Eingabesignal wird ein künstliches Neuron genutzt, welches das Signal entgegennimmt und es an die nächste Schicht weiterleitet.
Verarbeitung
In der Verarbeitung kommen die Gewichte zum Einsatz. Jedes Eingabesignal wird mit einem entsprechenden Gewicht multipliziert und summiert. Dadurch repräsentiert eine Zahl alle Eingabesignale. Neben den gewichteten Eingabesignalen wird zusätzlich ein Bias addiert. Wozu dieser Bias dient, wird klar, wenn man versteht, welche Art von Funktionen ein einfaches Perceptron lernen kann. Ein einfaches Perceptron ist auf lineare Funktionen beschränkt. Also Formeln der Form f(x) = a * x + b. Der Term a * x lässt sich aus der obigen Beschreibung relativ einfach ableiten: Es sind die Gewichte, die mit den Eingabewerten multipliziert werden. Um nun beliebige lineare Funktionen darstellen zu können, benötigen wir noch den Term b, um den y-Achsenabschnitt zu verändern. Dies wird durch die Ergänzung eines Bias erreicht. Somit ergibt sich nun das Ergebnis der Verarbeitung: Eine gewichtete Summe, welche alle Eingaben, inklusive des Bias, repräsentiert.
Ausgabesignal
Der letzte Schritt ist die Berechnung des Ausgabesignals. Hierbei wird die gewichtete Summe aus dem Verarbeitungsschritt mit einem Grenzwert verglichen. Die einfachste Funktion ist dabei die Heavyside-Funktion3. Sollte die gewichte Summe größer oder gleich dem Grenzwert sein, ist das Ausgabesignal 1, andernfalls 0.
Beispiel: Straßenschilderkennung
Nach der ganzen Theorie schauen wir uns nun ein relativ einfaches Beispiel an: Wir wollen ein Stoppschild von einem Einfahrtsverbotsschild unterscheiden. Die dominierende Farbe ist in beiden Fällen Rot, sie unterscheiden sich jedoch in der Form. Das Einfahrtsverbotsschild ist rund. Das Stoppschild ist achteckig. Ein Perceptron, welches nun Einfahrtsverbotsschilder erkennen soll, muss daher die Funktion lernen, die in der nachfolgenden Tabelle definiert ist.
| Rund (i) | Dominante Farbe:Rot (j) | Einfahrtsverbotsschild |
| Ja (1) | Ja (1) | Ja (Summe = 2) |
| Ja (1) | Nein (0) | Nein (Summe = 1) |
| Nein (0) | Ja (1) | Nein (Summe = 1) |
| Nein (0) | Nein (0) | Nein (Summe = 0) |
Zusätzlich nehmen wir an, dass wir die Heavyside-Funktion zur Aktivierung der Ausgabe verwenden. Dadurch lässt sich die Funktion, die das Perceptron abbilden soll folgendermaßen formulieren: i * w1 + j * w2 ≥ b, wobei b dem Bias entspricht. Durch Anwendung des Bias-Tricks4 können wir diese Funktion sogar noch etwas vereinfachen.
Durch Einführung eines zusätzlichen Biasgewichts (wb, wird laut Konvention immer auf 1 gesetzt) erhalten wir die Funktion: i * w1 + j * w2 + wb * -b ≥ 0. Mithilfe der obigen Tabelle, lassen sich nun die Gewichte und der Bias sehr einfach ablesen: Die Funktion soll nur dann erfüllt sein, wenn die Summe der Eingaben mindestens 2 ist. Daraus folgt, dass der Bias 2 ist.
Beide Werte (i, j) sind gleich wichtig und sollten daher auch gleich gewichtet in das Ergebnis eingehen. Daraus folgt, dass w1 und w2 auf 1 gesetzt werden können.
Die finale Funktion lautet dann: 1 * i + 1 * j – 2 ≥ 0. Wenn i und j 1 sind ergibt der linke Teil der Funktion 0, wodurch der Vergleich erfüllt ist und somit Ja durch die Aktivierungsfunktion zurückgegeben wird. Bei den verbleibenden Kombinationen aus i und j ist das Ergebnis immer kleiner als 0, wodurch Nein zurückgegeben wird.
Lernalgorithmus
Einer der entscheidendsten Fähigkeiten eines Perceptrons ist das Lernen von Funktionen. Aber was bedeutet Lernen in diesem Fall? Ein Perceptron lernt, indem es Fehler macht und versucht, diese zu korrigieren. Die Lernregel lässt sich dabei sehr einfach formulieren: wneu = walt + Δw, mit Δw = (y – ŷ) * x.
Das neue Gewicht ist also die Summe aus dem alten Gewicht und der Gewichtsänderung Δw. Dabei ist y die gewünschte Ausgabe, ŷ die berechnete Ausgabe und x die entsprechende Eingabe.
Orientieren wir uns an dem Beispiel aus dem vorherigen Kapitel. In diesem Fall setzen wir aber das Gewicht w1 auf 0, w2 hat weiterhin den Wert 1. Berechnen wir nun die Ausgabe für ein rundes und rotes Schild, erhalten wir die Aussage „Nein“, also einen Fehler. Dies lässt sich leicht überprüfen: 0 * 1 + 1 * 1 + 1 * -2 ≥ 0 ist nicht erfüllte, da -1 kleiner als 0 ist. Hier kommt nun die Lernregel ins Spiel. Die gewünschte Ausgabe (y) ist 1 und die berechnete Ausgabe (ŷ) ist 0. Daraus ergibt sich die Gewichtsänderung für w1: Δw = (1 – 0) * 1 = 1 und w2: Δw = (1 – 0) * 1 = 1.
Nach dem ersten Schritt sind die Gewichte also w1 = 1 und w2 = 2. Dadurch kommt es jedoch zu weiteren Fehlern, da das Perceptron nun immer “Ja“ ausgibt, sobald j = 1 ist. Daher wird diese Berechnung ebenfalls für die verbleibenden Eingabekombinationen durchgeführt, wodurch sich die Gewichte weiter anpassen.
Durch diese Anpassung erzeugt das Perceptron wieder das gewünschte Ergebnis.
Die Anwendung der Lernregel erscheint in diesem Beispiel trivial, da es sich um Boolsche-Werte handelt und nur ein Zyklus benötigt wird. Handelt es sich um eine Funktion auf reellen Zahlen, steigt die Anzahl der Zyklen deutlich und das Lernen wird komplexer.
KI-Winter
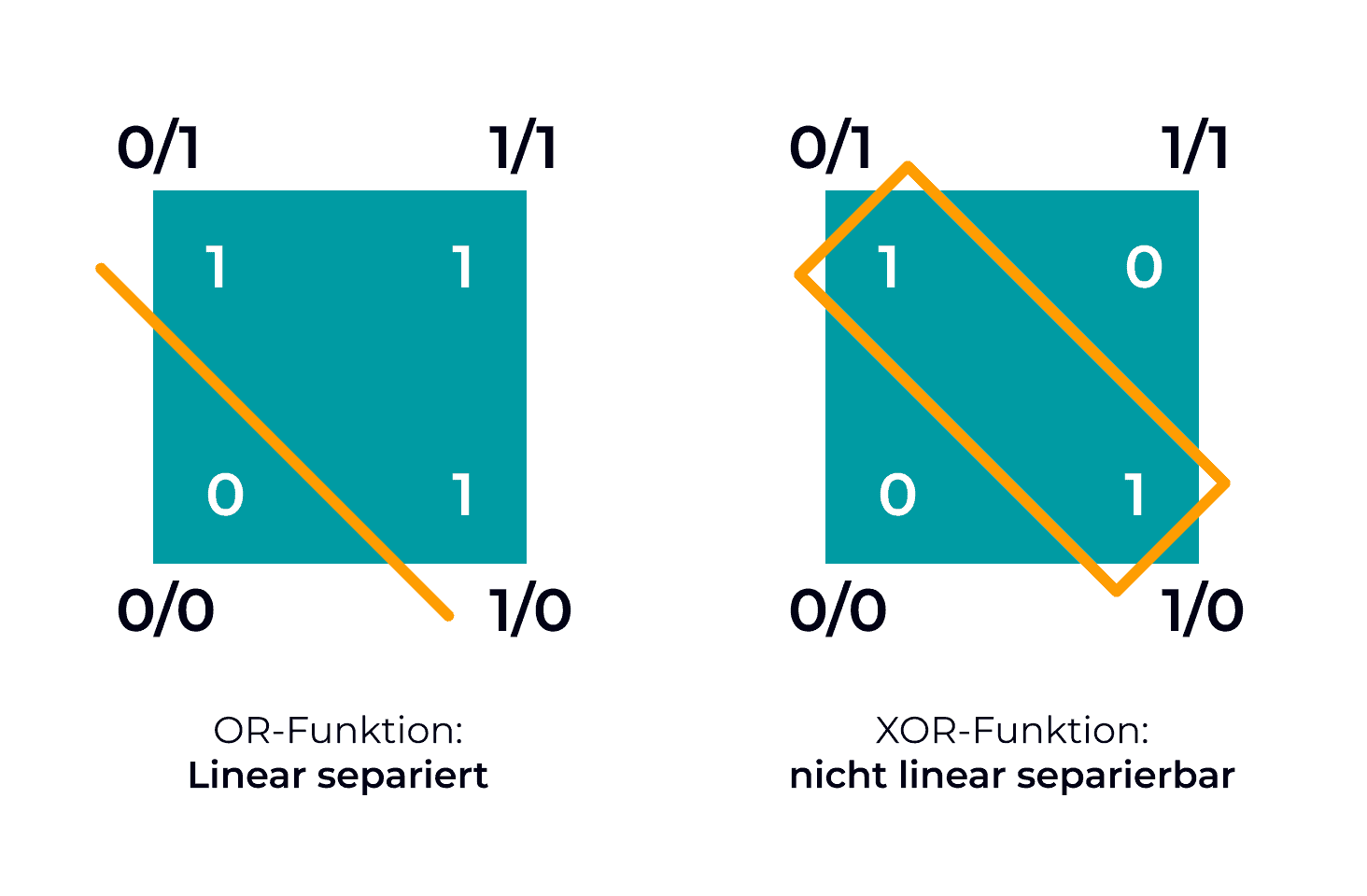
Diese bahnbrechende Technologie löste, wie heute ChatGPT, einen Hype aus und namenhafte Zeitungen wie die New York Times schrieben 1958: „the embryo of an electronic computer that [the Navy] expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence“5. Das Perceptron hat jedoch einen sehr großen Nachteil. Es kann nur Daten richtig klassifizieren, die linear trennbar sind.
Dadurch ist ein Perceptron nicht in der Lage den logischen Baustein XOR zu lernen. Dies wurde durch Marvin Minsky und Seymour Papert 1969 nachgewiesen6. Da nun die Limitationen des Perceptrons bekannt waren, wurde es für Forschende deutlich schwerer finanziert zu werden und das Interesse an dem Thema schwand deutlich. Dieser erste KI Winter dauerte bis in die Mitte der 1980er Jahre. Erst durch das Aufkommen von mehrlagigen Perceptren und Expertensystemen wurde wieder Interesse am Forschungsbereich KI geweckt.
Zusammenfassung
Das Perceptron war einer der ersten Schritte zu den modernen KI Systemen und Methoden, die wir fast täglich nutzen. Es war in der Lage, eine bestimmte Problemklasse (linear separierbare Daten) abzubilden und selbstständig die korrekte Klassifikation zu lernen. Die Fortschritte, die in den darauf folgenden Jahrzehnten erzielt wurden, konnten teilweise erst Jahre später richtig genutzt werden, da erst dann genügend Rechenkapazitäten zur Verfügung standen.
Quellen (Stand 11.04.2024):
- McCulloch, W. S. & Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. The Bulletin Of Mathematical Biophysics, 5(4), 115–133.
- The Organization of Behavior. (o. D.). Google Books.
- Wolfram Research, Inc. (o. D.). Heaviside Step Function — from Wolfram MathWorld.
- Der Bias – infaktum.de. (o. D.).
- Hardt, M. & Recht, B. (2022). Patterns, Predictions, and Actions: Foundations of Machine Learning. Princeton University Press.
- Minsky, Marvin, and Seymour A. Papert. Perceptrons, reissue of the 1988 expanded edition with a new foreword by Léon Bottou: an introduction to computational geometry. MIT press, 2017.